Sistema de los Números Reales

El conjunto de los números reales pertenece en matemáticas a la recta numérica que comprende a los números racionales y a los números irracionales. Esto quiere decir que incluyen a todos los números positivos y negativos, el símbolo cero, y a los números que no pueden ser expresados mediante fracciones de dos enteros que tengan como denominador a números no nulos (excluye al denominador cero).

El sistema de números reales se compone principalmente de dos grandes conjuntos, el de los números racionales que son aquellos que pueden ser expresados como la división de dos números enteros como 3/4, 3/5, incluso un número entero puede ser expresado como una fracción, ya que el número entero puede ser dividido en 1 sin cambiar su esencia, por ejemplo el número 8 puede ser expresado en fracción así 8/1; mientras que el otro gran conjunto del sistema de números reales es el de los números irracionales cuya representación decimal es expansiva, infinita y a periódica.

Los números irracionales son un conjunto en sí mismos pero, a su vez, los números racionales tienen subconjuntos que son: las fracciones no enteras con sus respectivas notaciones negativas; los números enteros; dentro de los números enteros están los negativos y los enteros positivos; estos últimos a su vez incluyen a los números naturales y al cero. Para aclarar esta conjunción, se puede graficar como en el diagrama de arriba.

Recta Real

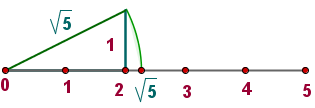
Los números reales pueden ser representados en la recta con tanta aproximación como queramos, pero hay casos en los que podemos representarlos de forma exacta. En la recta numérica, la representación de números reales se puede hacer con una exactitud aproximada, sin embargo, se pueden usar técnicas para representarlos de forma exacta

Leyes y Propiedades

1. Axioma Conmutativo de la Adición:

Para cualesquiera 2 números a y b :

a + b = b + a

Se puede conmutar o intercambiar, el orden de los números al sumarlos

2. Axioma Asociativo de la Adición:

Para cualesquiera números a, b y c :

(a + b) + c = a + (b + c)

Se pueden asociar los 3 números de 2 maneras diferentes al realizar la adición.

3. Axioma conmutativo de la multiplicación:

Para cualesquiera 2 números a y b :

a . b = b . a

4. Axioma Asociativo de la Multiplicación:

Para cualesquiera números a, b y c :

(a . b) . c = a . (b . c)

5. Axioma del Cero

Hay un único número 0 tal que:

a) 0 + a = a, para todo número a

b) 0 . a = 0, para todo número a

c) Si a . b = 0, entonces a = 0 o b = 0, o ambos son 0

6. Axioma del Uno

Hay un único número 1 tal que:

a) 0 + a = a, para todo número a

b) 0 . a = 0, para todo número a

c) Si a . b = 0, entonces a = 0 o b = 0, o ambos son 0

7. Axioma de la Suma

Si a y b son 2 números cualesquiera, hay un número único x tal que:

a = b + x

El número x es lo que comúnmente se representa con a - b

8. Axioma de la Multiplicación

Si a y b son 2 números cualesquiera, pero b es diferente de 0, entonces hay un número único x tal que:

b . x = a

x es lo que se acostumbra a designar con a/b

9. Axioma Distributivo

Para cualesquiera 3 números a, b y c :

ab + ac = a(b+ c)

Se dice que se obtiene a como factor común de la suma (o bien, se ha factorizado esta expresión)

10. Axioma del Elemento Opuesto

Un número es inverso del otro si al multiplicarlos obtenemos como resultado el elemento unidad

a . 1/a = 1

Regla de los Signos

Para operar con los números enteros es importante tener presentes las reglas de los signos:

• Para sumar dos elementos del conjunto W sólo se suman y su resultado está en W(la suma de positivos es positiva y con magnitud igual a la suma de las magnitudes), así 8 +23 = 31.

• Para sumar dos elementos del conjunto de enteros negativos, se suman sus magnitudes y al resultado se le asigna el signo negativo, -7 + (-13) = -20.

• La suma entre un número positivo y un negativo es igual a la resta de sus magnitudes con el signo correspondiente al de mayor magnitud, 36 + (-47)=-11.

• La multiplicación de números con el mismo signo (positivo o negativo) es igual al producto de los números con signo positivo, (5)(8) = (-5)(-8) = 40.

• La multiplicación de dos números con distinto signo es igual al producto de las magnitudes de los números y su signo es negativo, (7)(-8)=(-7)(8) = -56.

Valor Absoluto

En matemáticas, el valor absoluto o módulo de un número real es su valor numérico sin tener en cuenta su signo, sea este positivo (+) o negativo (-). La notación es la siguiente:

|-7| = 7, que se lee: el valor absoluto de -7 es 7.

|7| = 7, que se lee: el valor absoluto de 7 es 7.