
Cinemática
El desplazamiento de una partícula se define como su cambio en posición en algún intervalo de tiempo. Conforme la partícula se mueve desde una posición inicial Xi a una posición final Xf, su desplazamiento se conoce por
Δx = Xf - Xi
Tipos de movimiento

Teniendo en cuenta la forma de la trayectoria, el movimiento puede ser:
a) Rectilíneo: La posición del móvil con respecto al sistema de referencia elegido queda definida por una sola coordenada
b) Curvilíneo: Según el movimiento se produzca en el plano o en el espacio, la posición del móvil queda definida por dos o tres coordenadas respectivamente.
Teniendo en cuenta la constancia o no de la velocidad en el tiempo, el movimiento puede ser:
a) Uniforme: La velocidad del móvil se mantiene constante en dirección y sentido durante el intervalo de tiempo que dure el movimiento
b) Variado: La velocidad cambia en el tiempo debido a la variación de la rapidez (módulo de la velocidad), de la dirección o de ambos. De acuerdo a que la velocidad varíe en cantidades iguales en los mismos intervalos de tiempo o no, el movimiento es uniformemente variado o variado respectivamente.
Distancia es la longitud de una trayectoria seguida por una partícula
La distancia siempre se representa como un numero positivo, mientras que el desplazamiento puede ser positivo o negativo

Distancia
Velocidad Promedio
La velocidad promedio Vx,prom de una partícula se define como el desplazamiento Δx de la partícula dividido entre el intervalo de tiempo Δt durante el que ocurre dicho desplazamiento:
La velocidad promedio de una partícula que se mueve en una
dimensión es positiva o negativa, dependiendo del signo del
desplazamiento. (El intervalo de tiempo Δt siempre es positivo.)
La rapidez promedio Vprom de una partícula, una cantidad escalar,
se define como la distancia total recorrida dividida entre el intervalo
de tiempo total requerido para recorrer dicha distancia:



Rapidez Promedio
A diferencia de la velocidad promedio, la rapidez promedio no tiene dirección y siempre se expresa como un numero positivo
Movimiento rectilíneo uniforme (MRU)
Movimiento rectilíneo uniforme (MRU)
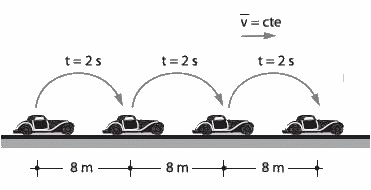
La velocidad es constante en módulo y dirección, por lo tanto la trayectoria es una recta y el móvil recorre distancias iguales en intervalos de tiempos iguales. En este movimiento:
a) La velocidad es constante v = cte , a = 0
b) La distancia recorrida crece proporcionalmente al
tiempo empleado.
Xf – Xi = v t
Xi indica la posición inicial del móvil con respecto al sistema de referencia elegido, es decir, representa la posición instantánea inicial del móvil para el instante inicial to en que comienza a medirse el tiempo.
Movimiento rectilíneo uniformemente variado (MRUV) o Movimiento uniformemente acelerado (MUA)
En este tipo de movimiento el módulo de la velocidad cambia en el tiempo en cantidades iguales, y por lo tanto la aceleración es constante. Considerando que Xi y Xi son la posición y velocidad iniciales, respectivamente, se tiene:

a)La aceleración es constante en módulo y dirección a = cte
b)La velocidad varia proporcionalmente al tiempo
Vf = Vi ± a t
c)El espacio recorrido crece proporcionalmente al tiempo al cuadrado.
Donde Vi = Velocidad inicial, Vf = velocidad final y d = distancia

Ejemplo: Una motocicleta esta parada en un semáforo que da acceso a una carretera. En el instante en el que el semáforo cambia a luz verde, le sobrepasa un automóvil que circula a una velocidad de 25m/s. El motorista arranca con una aceleración constante de 4 m/s2.
a) ¿Cuánto tarda la motocicleta en alcanzar al coche?
b) ¿Qué distancia han recorrido?
Documento del Ejercicio del video a continuación
Caída Libre

Es un tipo de movimiento uniformemente acelerado, donde la aceleración es constante y esta es igual a la gravedad, en el caso de la tierra, la gravedad promedio es de 9,8 m/s
Reemplazando en las ecuaciones anteriores:
Donde Xi = posición inicial, Xf = posición final, g = gravedad y h = altura

Ejemplo 1: Un observador se encuentra en una torre a 57,5 m del suelo; ve pasar una piedra disparada verticalmente hacia arriba desde el suelo y 6 s más tarde la vuelve a ver cuando viene de regreso.
a) ¿Con qué velocidad fue lanzada?
b) ¿A qué altura llego desde el suelo?
c) ¿Cuánto demoro en llegar hasta el observador?
Documento del Ejercicio del video a continuación
Ejemplo 2: Determina la profundidad de un pozo sobre el que se deja caer una piedra, y en el que se escucha el impacto sobre el agua después de transcurridos 1.5 s, teniendo en cuenta que la velocidad del sonido es 340 m/s.
Documento del Ejercicio del video a continuación
Movimiento Parabólico y Semiparabólico

En el movimiento curvilíneo, la velocidad del móvil varía de dirección en el tiempo, mientras que el módulo puede permanecer constante o cambiar en el tiempo. Por ello, existe siempre una aceleración normal que da cuenta del cambio de dirección de la velocidad
Las ecuaciones del m.r.u. para el eje x


Las ecuaciones del m.r.u.a. para el eje y
Ejemplos:
Ejemplo 1: Se dispara una flecha con una velocidad de 25 m/s y un ángulo de elevación de 35º con respecto a la horizontal.
Determinar:
a) El tiempo que tarda en llegar al punto más alto.
b) Tiempo total en el aire.
c) Alcance horizontal.
d) Altura máxima lograda
Ejemplo 2: Una bala de cañón se dispara con una velocidad inicial de 705 ft/s y con un ángulo de elevación de 25º sobre la horizontal
Determina:
a) El tiempo requerido para alcanzar su altura máxima.
b) El alcance horizontal
c) Su posición y velocidad después de 15 s
Excel del Ejercicio del video a continuación
Ejemplo 3: Una bala de cañón se dispara horizontalmente con una velocidad inicial de 160 m/s desde lo alto de un acantilado de 309 m de altura sobre el nivel del mar, tal como se muestra en la figura.
Determina:
a) ¿Qué tiempo tardará la bala en caer en el mar?
b) ¿Cuál será la distancia horizontal del pie del acantilado al punto de impacto de la bala.
c) ¿Cuáles son las componentes horizontal y vertical de la velocidad de la bala cuando cae en el mar.
Ejemplo 4: Un avión de rescate en Alaska deja caer un paquete de provisiones a un grupo de exploradores extraviados, como se muestra en la figura. Si el avión viaja horizontalmente a 40 m/seg. Y a una altura de 100 metros sobre el suelo. ¿Dónde cae el paquete en relación con el punto en que se soltó?
El desarrollo de los 2 anteriores ejercicios se puede observar en el siguiente video:
Excel del Ejercicio del video a continuación
Ejemplo 5: En un bar local, un cliente hace deslizar un tarro vacío de cerveza sobre la barra para que vuelvan a llenarlo. El cantinero esta momentáneamente distraído y no ve el tarro, el cual cae de la barra y golpea el piso a 1,4 metros de la base de la misma. Si la altura de la barra es 0,86 metros..
Determina:
a) ¿Con que velocidad abandono el tarro la barra?
b) ¿Cual fue la velocidad del tarro al chocar con el piso?
Ejercicio propuesto: Un jugador de básquetbol de 2 metros de altura lanza un tiro a la canasta situada a 3,05 m de altura, desde una distancia horizontal de 10 metros. Si tira a un ángulo de 40 grados, con la horizontal, ¿Con que velocidad inicial debe tirar de manera que el balón entre al aro sin golpear el tablero?
El desarrollo del ejercicio 5 se puede observar en el siguiente video:
Excel del Ejercicio del video a continuación
El desarrollo del ejercicio propuesto del anterior video se puede observar en el siguiente:
Excel del Ejercicio del video a continuación
Ejemplo 6: Un avión vuela horizontalmente con velocidad Va = 1200 km/h a una altura de 2.100 m, suelta una bomba que debe dar en un barco cuya velocidad es Vb = 45 km/h con igual dirección y sentido. Determinar:
a) ¿Qué tiempo tarda la bomba en caer?
b) ¿Con qué velocidad llega la bomba al barco?
c) ¿Qué distancia recorre el barco desde el lanzamiento hasta el impacto? ¿Lo golpearía la Bomba?
El desarrollo del ejercicio 5 se puede observar en el siguiente video:
Excel del Ejercicio del video a continuación
Ejemplo 7: Desde la azotea de un edificio se lanza una piedra hacia arriba a un ángulo de 30 grados con respecto de la horizontal y con una velocidad inicial de 20 m/s. Como muestra la figura. Si la altura del edificio es 45 m. ¿Cuánto tiempo permanece la pierda en vuelo?
El desarrollo del ejercicio 5 se puede observar en el siguiente video: